- Autor admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:26.
- Última modificação 2025-01-23 15:33.

Exemplos da Proporção Áurea podem ser encontrados em todos os lugares na arquitetura clássica, nas obras de arte, na natureza e até na música. Esta expressão de proporção, também conhecida como Proporção Divina, oferece uma composição harmoniosa através da aplicação de um número irracional (1.618) no design, tanto natural como feito pelo homem. Provavelmente, você não conhece a matemática por trás da beleza da Proporção Áurea porque ela produz objetos e músicas que você naturalmente achará agradáveis, sem precisar de qualquer explicação.
Proporção Áurea na Arquitetura
A Proporção Áurea cria uma beleza quase perfeita na natureza e na arte. Quando você começa a procurar exemplos de Proporção Áurea na vida cotidiana, pode se surpreender com os muitos casos em que ela tem sido usada para criar muitos edifícios e estruturas monumentais. Quando a Proporção Áurea é usada na arquitetura, diz-se que o edifício foi criado usando "arquitetura sagrada". Ao aplicar o cálculo da Proporção Áurea a um quadrado, arquitetos e designers são capazes de criar o Retângulo Áureo, que se acredita ter as proporções mais esteticamente agradáveis ao olho humano.
Exemplo de retângulo dourado: O Partenon

Phidias, o escultor grego, utilizou a Proporção Áurea em seu trabalho, principalmente quando começou a trabalhar com as faixas que esculpiu logo acima das colunas do Partenon. Também é importante observar que o valor numérico atribuído à Proporção Áurea, Phi, foi nomeado em sua homenagem.
Se você medir as dimensões do exterior do Partenon, descobrirá que ele não apenas forma um Retângulo Dourado, mas também há muitos Retângulos Dourados entre as colunas. Esta estrutura sagrada é um belo exemplo da Proporção Áurea na arquitetura.
Exemplo do Triângulo Dourado: Grande Pirâmide de Gizé
A Proporção Áurea, o Retângulo Áureo e o Triângulo Dourado podem ser encontrados na perfeição de uma das Sete Maravilhas do Mundo, a Grande Pirâmide de Gizé. Para encontrar a Proporção Áurea, você precisará dividir a base quadrada da pirâmide pela metade e desenhar uma linha vertical subindo pelo centro da pirâmide. Quando isso está conectado a um lado angular da pirâmide, você pode ver facilmente como ele forma o Triângulo Dourado com uma proporção de 1,618, a Proporção Áurea.
Outros exemplos arquitetônicos
Você pode encontrar muitos exemplos de arquitetura sagrada antiga e moderna e edifícios da Proporção Áurea.
- Catedral de Chartres - Centro, França
- Notre Dame - Paris, França
- Pártico das Donzelas - Acrópole, Atenas
- Taj Mahal - Agra, Índia
- Edifício das Nações Unidas - Nova York, Nova York
Proporção áurea em exemplos de arte
Você pode encontrar muitos exemplos de mestres pintores que usaram a Proporção Áurea. Estas obras de perfeição foram criadas usando a proporção de Retângulos Dourados e Triângulos Dourados. A arte criada com base no Retângulo Dourado mostra-se mais agradável ao olho humano. É um dos mistérios que cerca esse retângulo perfeito e a Proporção Áurea.
Proporção Áurea na Arte

Exemplos de arte com proporção áurea incluem:
- Leonardo Di Vinci - Mona Lisa, Homem Vitruviano
- Botticelli - Nascimento de Vênus
- Michelangelo - Sagrada Família, 'David'
- Rafael - Crucificação
- Rembrandt - Auto-retrato
- Salvador Dali - O Sacramento da Última Ceia, A Persistência da Memória
Usando a Proporção Áurea na Composição Artística
Dentro de um Retângulo Dourado estão certas áreas que são consideradas mais atraentes visualmente do que outras áreas. Esses pontos são descobertos traçando uma linha do canto inferior do retângulo até o canto oposto e repetindo-a com o outro canto inferior. Essas linhas se cruzarão exatamente no centro do Retângulo Dourado. Em seguida, meça o meio de cada linha começando no ponto central. Esses quatro pontos são chamados de olhos do retângulo (proporção áurea). O principal ponto focal da pintura é então desenhado ou pintado dentro desses pontos de interesse (proporções).
Proporção Áurea na Música

A música é composta por valores numéricos e quando a Proporção Áurea é usada para criar uma peça musical, ela se torna um exemplo vivo de matemática. A Sequência de Fibonacci também prevalece na música:
- Existem oito notas em uma escala.
- A terceira e a quinta notas são a base dos acordes.
- A duração, ou oitava, de qualquer nota é de 13 notas.
A sequência continua ao longo de uma peça musical e se torna mais complexa à medida que atinge a Proporção Áurea.
Compositores que usaram a proporção áurea
Alguns dos compositores clássicos mais conhecidos usaram a Proporção Áurea e a Sequenciação de Fibonacci em suas peças musicais, incluindo Bach, Beethoven, Chopin e Mozart. Alguns compositores modernos como Casey Mongoven exploraram a Proporção Áurea em suas músicas.
Exemplos de proporção áurea na natureza

Onde a Proporção Áurea é encontrada na natureza? Está na Espiral Áurea ou Fibonacci, que pode ser criada usando a Proporção Áurea. Este é um fenômeno encontrado extensivamente no mundo natural. As folhas de uma planta crescem tanto quanto possível, podendo subir em espiral no caule. Uma nova folha só se forma após a formação da folha seguinte.
- Cactos espirais
- Galáxias espirais
- Girassóis
Flores com a sequência de Fibonacci
Algumas flores possuem pétalas que seguem a Sequência de Fibonacci:
- Três pétalas:Íris, lírio, orquídeas, trílio
- Cinco pétalas: Botões de ouro, gerânios, hibisco, ipomeia, capuchinha
- Oito pétalas: Delphiniums
- 13 pétalas: Certas variedades de margaridas, ambrósia, calêndula
Espiral de Fibonacci em Pinhas

Dependendo da espécie de árvore, você também pode ver a Proporção Áurea em ação dentro de uma série de números de Fibonacci em pinhas. Você pode encontrar uma série de oito espirais de um lado da pinha e 13 espirais do outro. Outro padrão de pinha tem cinco espirais de um lado e oito do outro.
Proporção Áurea em Humanos
Essa proporção também é importante não apenas para a forma como os humanos veem uns aos outros, mas também para o modo como seus corpos funcionam e para seu DNA.
DNA revela a proporção áurea
Um dos exemplos mais surpreendentes da Proporção Áurea é encontrado na estrutura do DNA humano. Isso pode ser visto em uma única seção transversal do DNA que revela que a dupla hélice do DNA forma um decágono. Esta é uma combinação de dois pentágonos, girados 36 graus um do outro, formando a dupla hélice do DNA. A própria espiral de dupla hélice forma um pentágono. Mesmo uma única molécula de DNA revela uma base da Seção Áurea ou Proporção Divina.
A matemática por trás da proporção áurea
Encontrar a Proporção Áurea na vida real é simples, pois ela aparece ao seu redor. É um truísmo matemático usado para definir o que é comumente conhecido como o número perfeito encontrado na natureza, que foi duplicado e imitado pelos humanos durante séculos. A beleza simplista deste número disfarça a sua complexidade na execução. Para entender a teoria por trás da Proporção Áurea, você deve primeiro explorar a Sequenciação Fibonacci da proporção.
Sequência de Fibonacci e a Proporção Áurea
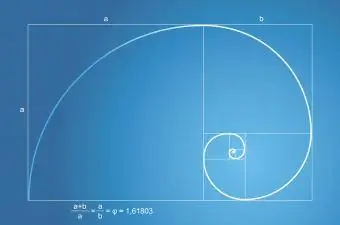
A Sequência ou Série de Fibonacci tem uma relação com a Proporção Áurea. A Série Fibonacci aparece no número de folhas de uma planta e no número de pétalas de uma flor. A espiral de Fibonacci, encontrada na natureza, sempre faz parte de um retângulo áureo com proporção áurea.
A matemática da Série Fibonacci é simples:
- A sequência começa com 0 e 1.
- Basta somar os dois últimos números para obter o próximo número da série.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 e assim por diante.
- Este exemplo da Série Fibonacci se torna: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 e assim por diante.
A relação de Fibonacci com a Proporção Áurea é percebida quando ela é adicionada cada vez mais. Quanto mais você adiciona a série, mais próximo você chega da Proporção Áurea.
Criando um retângulo e triângulo dourado
Para criar um Retângulo Dourado com a Sequência de Fibonacci, você começa com um quadrado. Você começará a construir um retângulo adicionando outro quadrado ao quadrado original. Lembre-se de usar a fórmula: 0+1=1 é o primeiro quadrado, 1+1=2 - você adicionará outro quadrado.1+2=3 você adicionará três quadrados e a seguir, 2+3=5, você adicionará cinco quadrados. Você continuará adicionando quadrados e eventualmente formando um retângulo dourado.
Um Triângulo Dourado pode ser criado dividindo um Retângulo Dourado ao meio de um canto ao canto oposto. Isso cria um triângulo onde seus três lados ou ângulos têm uma proporção de 2:2:1, o que significa que os dois lados longos têm comprimento igual e o ângulo curto tem exatamente metade do comprimento dos dois lados mais longos.
Proporção áurea no mundo real
A Proporção Áurea é frequentemente chamada de Proporção Divina devido à sua proeminência na natureza e nos corpos humanos. A descoberta de que a Proporção Áurea está presente em tantos seres vivos fomentou a reverência por essa proporção mágica e continua a ser uma inspiração para artistas e criadores hoje.






